 |
| Lógica Proposicional - Construção de Tabela-Verdade de uma Fórmula com Árvore de Decomposição |
No artigo anterior aprendemos a criar uma
árvore de composição e decomposição de uma fórmula e com isso possuímos
condições de construir a tabela-verdade de qualquer fórmula dada.
Vimos que, dada uma expressão proposicional, e dados os valores lógicos das
proposições simples que a compõe, podemos, com a ordem de precedência,
calcular o valor lógico da expressão dada. No entanto, estaremos interessados,
muitas vezes, no conjunto de valores lógicos que a expressão pode assumir,
para quaisquer valores lógicos das proposições componentes.
Caso o leitor não tenha se adaptado a tabela-verdade de cada conectivo, veja o
artigo
Lógica Proposicional - Conectivo e Tabela-Verdade.
Serão apresentados duas técnicas para a construção da tabela-verdade de uma
fórmula, onde as mesmas serão revisadas nos artigos de
tautologias,
contradição,
contingência,
negação
e
equivalência.
Construção da tabela-verdade com uma árvore
Construção da tabela-verdade:
|
Passos
|
Instruções
|
|---|---|
|
01
|
Construa a árvore de decomposição da fórmula.
|
|
02
|
Veja quais e quantas são as fórmulas atômicas.
|
|
03
|
Escreva em ordem alfabética as atômicas e trace colunas para cada uma
delas.
|
|
04
|
Trace $$2 ^ n$$ linhas, sendo $$n$$ o número de atômica.
|
|
05
|
Agora, olhe para a árvore de decomposição. Se houver apenas um ramo,
olhe-as de baixo para cima, e escreva cada uma das subfórmulas da
esquerda para a direita (sentido usual de escrita), cada uma em uma
coluna separada.
|
|
06
|
Se a árvore apresentar dois ramos, considere primeiro o ramo da
esquerda e escreva cada uma das subfórmulas começando pelas atômicas,
de baixo para cima, transportando-as na primeira linha e escrevendo-as
da esquerda para a direita (sentido usual de escrita), cada uma em uma
coluna separada. Passe à coluna da direita e faça o mesmo, até esgotar
todas as subfórmulas e chegar na última fórmula.
|
Preenchimento da tabela-verdade:
|
Passos
|
Instruções
|
|---|---|
|
01
|
Olhemos inicialmente todas as colunas das atômicas.
|
|
02
|
Na primeira coluna, preenchemos a primeira metade com V e a outra
metade com F.
|
|
03
|
Na segunda coluna, para cada metade de V da primeira coluna,
preenchemos a primeira metade com V e a outra metade com F. Na outra
metade F, ainda da primeira coluna, preenchemos a primeira metade com
V e a outra metade com F.
|
|
04
|
Nas demais colunas, repete-se o processo anterior, para cada bloco de
V e de F, até chegar à última coluna que deve apresentar-se assim: V,
F, V, F, etc.
|
Preenchimento das demais colunas:
|
Passos
|
Instruções
|
|---|---|
|
01
|
A tabela já está pronta para que a primeira coluna após as atômicas
seja preenchida, olhando-se a tabela-verdade da fórmula da coluna.
|
|
02
|
Repete-se o processo acima, pois a tabela já dá a sequência de
preenchimento.
|
|
03
|
Como na última coluna deve figurar a fórmula complexa, a
tabela-verdade da fórmula está feita.
|
Vejamos dois exemplos para que o leitor se familiarize com este conceito.
Dada a fórmula $$[\text{A}$$ $$\rightarrow$$ $$(\text{B}$$ $$\vee$$
$$\text{C})]$$. Construa a tabela-verdade.
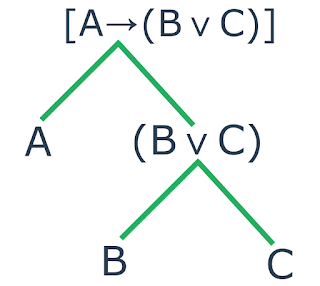
Seguindo os passos de construção, devemos, inicialmente, construir a árvore de
decomposição da fórmula em questão. Logo, teremos:
|
| Decomposição de uma fórmula do tipo implicação |
Após a construção da árvore, devemos observar quais e quantas fórmulas
atômicas a fórmula complexa possui. No nosso caso, as fórmulas atômicas são:
$$\text{A}$$, $$\text{B}$$ e $$\text{C}$$.
Com a identificação e a organização, em ordem alfabética, das fórmulas
atômicas, podemos traçar as colunas para cada uma delas. Logo, teremos:
|
$$\text{A}$$
|
$$\text{B}$$
|
$$\text{C}$$
|
Segundo o quarto passo, devemos traçar oito linhas, porque possuímos três
fórmulas atômicas e a quantidade de linhas de uma tabela é definida pela
fórmula $$2 ^ n$$, onde $$n$$ é a quantidade de fórmulas atômicas. Logo,
teremos:
|
$$\text{A}$$
|
$$\text{B}$$
|
$$\text{C}$$
|
|
-
|
-
|
-
|
|
-
|
-
|
-
|
|
-
|
-
|
-
|
|
-
|
-
|
-
|
|
-
|
-
|
-
|
|
-
|
-
|
-
|
|
-
|
-
|
-
|
|
-
|
-
|
-
|
Os passos quinto e sexto nos instrui a olhar os ramos da árvore e verificar se
a mesma é possuidora de um ou dois ramos. Na fórmula em questão ela é
possuidora de dois, então seguiremos o sexto passo.
Observemos inicialmente o ramo da esquerda e percebemos que ele é constituído
de uma fórmula atômica, então não faremos nada. Ele possui apenas uma fórmula
atômica, mas o ramo do lado direito é possuidor de uma subfórmula e que a
mesma é possuidora de duas atômicas. Escreveremos a subfórmula do ramo direito
em uma coluna na tabela. Logo, teremos:
|
$$\text{A}$$
|
$$\text{B}$$
|
$$\text{C}$$
|
$$(\text{B}$$ $$\vee$$ $$\text{C})$$
|
|
-
|
-
|
-
|
-
|
|
-
|
-
|
-
|
-
|
|
-
|
-
|
-
|
-
|
|
-
|
-
|
-
|
-
|
|
-
|
-
|
-
|
-
|
|
-
|
-
|
-
|
-
|
|
-
|
-
|
-
|
-
|
|
-
|
-
|
-
|
-
|
Como a subfórmula $$(\text{B}$$ $$\vee$$ $$\text{C})$$ é constituída de apenas
fórmulas atômicas, devemos agora escrever a fórmula complexa, $$[\text{A}$$
$$\rightarrow$$ $$(\text{B}$$ $$\vee$$ $$\text{C})]$$. Logo, teremos:
|
$$\text{A}$$
|
$$\text{B}$$
|
$$\text{C}$$
|
$$(\text{B}$$ $$\vee$$ $$\text{C})$$
|
$$[\text{A}$$ $$\rightarrow$$ $$(\text{B}$$ $$\vee$$ $$\text{C})]$$
|
|
-
|
-
|
-
|
-
|
-
|
|
-
|
-
|
-
|
-
|
-
|
|
-
|
-
|
-
|
-
|
-
|
|
-
|
-
|
-
|
-
|
-
|
|
-
|
-
|
-
|
-
|
-
|
|
-
|
-
|
-
|
-
|
-
|
|
-
|
-
|
-
|
-
|
-
|
|
-
|
-
|
-
|
-
|
-
|
Devemos preencher a metade da coluna da primeira atômica de V e a outra de F.
Observe:
|
$$\text{A}$$
|
$$\text{B}$$
|
$$\text{C}$$
|
$$(\text{B}$$ $$\vee$$ $$\text{C})$$
|
$$[\text{A}$$ $$\rightarrow$$ $$(\text{B}$$ $$\vee$$ $$\text{C})]$$
|
|
V
|
-
|
-
|
-
|
-
|
|
V
|
-
|
-
|
-
|
-
|
|
V
|
-
|
-
|
-
|
-
|
|
V
|
-
|
-
|
-
|
-
|
|
F
|
-
|
-
|
-
|
-
|
|
F
|
-
|
-
|
-
|
-
|
|
F
|
-
|
-
|
-
|
-
|
|
F
|
-
|
-
|
-
|
-
|
Como a primeira coluna possui oito linhas, com exceção do cabeçalho, as quatro
primeiras são V e as demais são F.
O terceiro passo de preenchimento nos diz que na segunda coluna, para cada
metade de V da primeira coluna, preenchemos a primeira metade com V e a outra
metade com F. Vejamos:
|
$$\text{A}$$
|
$$\text{B}$$
|
$$\text{C}$$
|
$$(\text{B}$$ $$\vee$$ $$\text{C})$$
|
$$[\text{A}$$ $$\rightarrow$$ $$(\text{B}$$ $$\vee$$ $$\text{C})]$$
|
|
V
|
V
|
-
|
-
|
-
|
|
V
|
V
|
-
|
-
|
-
|
|
V
|
F
|
-
|
-
|
-
|
|
V
|
F
|
-
|
-
|
-
|
|
F
|
V
|
-
|
-
|
-
|
|
F
|
V
|
-
|
-
|
-
|
|
F
|
F
|
-
|
-
|
-
|
|
F
|
F
|
-
|
-
|
-
|
Observe que a segunda coluna "pega" a metade composta por V da primeira coluna
e preenche a metade da metade com V e a outra metade com F. O procedimento é
repetido para a metade composta por F.
Segundo o quarto passo, devemos repetir o processo do terceiro, mas com base
no antecessor (segunda coluna). Logo, teremos:
|
$$\text{A}$$
|
$$\text{B}$$
|
$$\text{C}$$
|
$$(\text{B}$$ $$\vee$$ $$\text{C})$$
|
$$[\text{A}$$ $$\rightarrow$$ $$(\text{B}$$ $$\vee$$ $$\text{C})]$$
|
|
V
|
V
|
V
|
-
|
-
|
|
V
|
V
|
F
|
-
|
-
|
|
V
|
F
|
V
|
-
|
-
|
|
V
|
F
|
F
|
-
|
-
|
|
F
|
V
|
V
|
-
|
-
|
|
F
|
V
|
F
|
-
|
-
|
|
F
|
F
|
V
|
-
|
-
|
|
F
|
F
|
F
|
-
|
-
|
Observe que a terceira coluna "pega" a metade composta por V da segunda coluna
e preenche a metade da mesma com V e a outra metade com F. O procedimento é
repetido para as demais metades.
Após a construção da tabela e o preenchimento inicial, podemos preencher as
demais colunas que designam as fórmulas.
Seguindo o primeiro passo de preenchimento das demais colunas, devemos olhar a
tabela-verdade de cada conectivo e preencher as lacunas restantes com base no
valor verdade das atômicas. Caso o leitor não se lembre da tabela-verdade de
cada conectivo, clique
aqui. Logo, teremos:
|
$$\text{A}$$
|
$$\text{B}$$
|
$$\text{C}$$
|
$$(\text{B}$$ $$\vee$$ $$\text{C})$$
|
$$[\text{A}$$ $$\rightarrow$$ $$(\text{B}$$ $$\vee$$ $$\text{C})]$$
|
|
V
|
V
|
V
|
V
|
-
|
|
V
|
V
|
F
|
V
|
-
|
|
V
|
F
|
V
|
V
|
-
|
|
V
|
F
|
F
|
F
|
-
|
|
F
|
V
|
V
|
V
|
-
|
|
F
|
V
|
F
|
V
|
-
|
|
F
|
F
|
V
|
V
|
-
|
|
F
|
F
|
F
|
F
|
-
|
Observação importante: as cores servem, apenas, para que o leitor possa
se familiarizar com a aplicação. Em uma tabela-verdade não se utiliza cores
distintas.
A subfórmula trabalhada é $$(\text{B}$$ $$\vee$$ $$\text{C})$$ e é constituída
das atômicas $$\text{B}$$ e $$\text{C}$$, então devemos trabalhar linha por
linha, obedecendo o valor verdade das atômicas. Por exemplo, na segunda linha,
destacada em vermelho, as atômicas $$\text{B}$$ e $$\text{C}$$ são possuidoras
do valor verdade verdadeiro, segundo a
tabela-verdade da disjunção inclusiva, a sentença $$(\text{B}$$
$$\vee$$ $$\text{C})$$ é falso se e somente se as proposições simples
$$\text{B}$$ e $$\text{C}$$ forem possuidoras do valor verdade falso, e não é
isso que ocorre na primeira linha, consequentemente a sentença $$(\text{B}$$
$$\vee$$ $$\text{C})$$ é possuidora do valor verdade verdadeiro.
Tomemos como outro exemplo a última linha da tabela. Ela mostra que as
atômicas $$\text{B}$$ e $$\text{C}$$ são possuidoras do valor verdade falso,
então a sentença $$(\text{B}$$ $$\vee$$ $$\text{C})$$, segundo a
tabela-verdade da disjunção inclusiva, é possuidora, também, do valor
verdade falso.
O segundo passo nos informa que devemos repetir o processo do primeiro. Logo,
teremos:
|
$$\text{A}$$
|
$$\text{B}$$
|
$$\text{C}$$
|
$$(\text{B}$$ $$\vee$$ $$\text{C})$$
|
$$[\text{A}$$ $$\rightarrow$$ $$(\text{B}$$ $$\vee$$ $$\text{C})]$$
|
|
V
|
V
|
V
|
V
|
V
|
|
V
|
V
|
F
|
V
|
V
|
|
V
|
F
|
V
|
V
|
V
|
|
V
|
F
|
F
|
F
|
F
|
|
F
|
V
|
V
|
V
|
V
|
|
F
|
V
|
F
|
V
|
V
|
|
F
|
F
|
V
|
V
|
V
|
|
F
|
F
|
F
|
F
|
V
|
Tomemos como exemplo a quinta linha. Segundo a tabela-verdade da implicação, a
sentença $$[\text{A}$$ $$\rightarrow$$ $$(\text{B}$$ $$\vee$$ $$\text{C})]$$
toma o valor verdade falso se e somente se o antecedente, $$\text{A}$$, é
verdadeiro e o consequente, $$(\text{B}$$ $$\vee$$ $$\text{C})$$, é falso. Com
isso, na quinta linha, a fórmula $$[\text{A}$$ $$\rightarrow$$ $$(\text{B}$$
$$\vee$$ $$\text{C})]$$ é atribuída com o valor verdade falso.
E com isso, concluímos a construção da tabela-verdade da fórmula $$[\text{A}$$
$$\rightarrow$$ $$(\text{B}$$ $$\vee$$ $$\text{C})]$$, porque o terceiro passo
nos diz: "como na última coluna deve figurar a fórmula complexa, a
tabela-verdade da fórmula está feita".
Não podemos nos esquecer que o tipo de uma fórmula é determinado pelo
conectivo que dá origem ao primeiro ramo. No exemplo finalizado, a sentença é
do tipo implicação.
Dada a fórmula $$\{\neg$$$$[[(\neg$$$$\text{B})$$ $$\wedge$$
$$(\neg$$$$(\neg$$$$\text{A}))]$$ $$\leftrightarrow$$
$$[\neg$$$$(\neg$$$$(\text{B}$$ $$\vee$$ $$\text{C})$$$$)]]\}$$. Construa a
tabela-verdade.
Seguindo os passos de construção, devemos inicialmente construir a árvore de
decomposição da fórmula em questão. Logo, teremos:
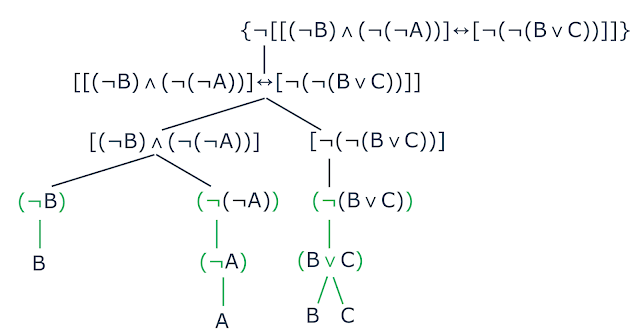 |
| Decomposição de uma fórmula do tipo negação |
Para construir a tabela-verdade do segundo exemplo, seria necessário uma longa
explicação escrita e para não deixar o leitor cansado, estive gravando uma
explicação e construção da tabela-verdade. Veja o vídeo logo abaixo:
O que você aprendeu
Este artigo teve o objetivo de demostrar a construção de uma tabela-verdade de
fórmula com o uso de uma árvore binária de decomposição, foram usados dois
exemplos e uma vídeo aula para facilitar o aprendizado. Especificamente, você
aprendeu:
- Criação de uma tabela-verdade de uma fórmula dada.
- Para que serve uma árvore de decomposição.
Continua em
Continuação de
Veja todos os artigos em
Lista de Artigos sobre Lógica Proposicional
Lista de Artigos sobre Lógica Proposicional
Referência Bibliográfica
ABE, J. M; SCALZITTI, A; FILHO, J. I. S. Introdução à Lógica para a Ciência da Computação. 2. ed. São Paulo: Arte & Ciência, 2002. 247 p.
Para citar esse artigo:
 Pular para o conteúdo principal
Pular para o conteúdo principal
Comentários
Postar um comentário